286. Walls and Gates
Question
Given a map containing a door (0), a wall (-1) and a space (INF). Calculate the distance from each space to the nearest door (or the closest distance to the door).
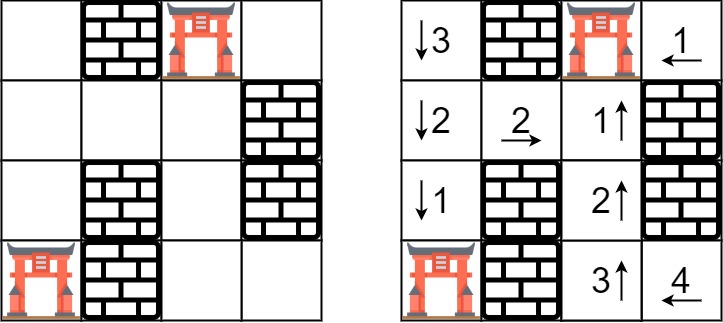
Input: rooms = [[2147483647,-1,0,2147483647],[2147483647,2147483647,2147483647,-1],[2147483647,-1,2147483647,-1],[0,-1,2147483647. 2147483647]]
Output: [[3,-1,0,1],[2,2,1,-1],[1,-1,2,-1],[0,-1,3,4]]
Algorithm
This topic looks like it goes with the flood fill algorithm. Traverse the map, do bfs after encountering a door, figure out the distance to each spatial grid, and record the minimum value. This is for each door to start the bfs, visited are to reset, because spaces can be repeated to go.
But the implementation of this algorithm as code 1, the final space complexity will be O(m*n*m*n), because traversing the map once is O(mn), in the traversal of each door is O(mn). The platform will award TEL.
The reference answer gives an idea that can bring down the time complexity to O(mn).
The specific idea is to record all the gates in the queue at the beginning and then start bfs, so that the result obtained is the minimum value. For example, the [1, 0] position in the example, when the first time to take the value from the queue, that is, the first level of traversal, will take the [2, 0] position above the [3, 0] door position and the [1, 2] below the door [0, 2], the second round of traversal, the [2, 0] position next will traverse to the [1, 0] position, so the distance is already the shortest.
It can be understood that each round of traversal is a circle (distance plus one) from the door outward, and the distance is the shortest bit. When other gates encounter this position, as well as the value and the shortest, he will not go back to assign a value.
This question is not like the traditional flood fill algorithm because we are not calculating connectivity, but for each empty position to do the shortest distance calculation, the entire board of empty positions will be repeated, so you can start from all the roots (gates) at the same time, which will save time. And for question 200, calculating the number of islands, we count them one by one because the current connected islands will not be counted repeatedly after they have been counted.
Code 1
class Solution {
public void wallsAndGates(int[][] rooms) {
if (rooms == null || rooms.length == 0 || rooms[0] == null || rooms[0].length == 0) {
return;
}
for (int i = 0; i < rooms.length; i++) {
for (int j = 0; j < rooms[0].length; j++) {
boolean[][] visited = new boolean[rooms.length][rooms[0].length];
if (rooms[i][j] == 0) {
bfs(rooms, i, j, visited);
}
}
}
}
private void bfs(int[][] rooms, int i, int j, boolean[][] visited) {
visited[i][j] = true;
Queue<int[]> queue = new LinkedList<>();
queue.offer(new int[]{i, j});
int level = 0;
while (!queue.isEmpty()) {
level++;
int size = queue.size();
for (int x = 0; x < size; x++) {
int[] pos = queue.poll();
int row = pos[0];
int col = pos[1];
if (row - 1 >= 0 && rooms[row-1][col] != -1 && !visited[row-1][col]) {
visited[row-1][col] = true;
queue.offer(new int[]{row-1, col});
rooms[row-1][col] = Math.min(rooms[row-1][col], level);
}
if (row + 1 < rooms.length && rooms[row+1][col] != -1 && !visited[row+1][col]) {
visited[row+1][col] = true;
queue.offer(new int[]{row+1, col});
rooms[row+1][col] = Math.min(rooms[row+1][col], level);
}
if (col - 1 >= 0 && rooms[row][col-1] != -1 && !visited[row][col-1]) {
visited[row][col-1] = true;
queue.offer(new int[]{row, col-1});
rooms[row][col-1] = Math.min(rooms[row][col-1], level);
}
if (col + 1 < rooms[0].length && rooms[row][col+1] != -1 && !visited[row][col+1]) {
visited[row][col+1] = true;
queue.offer(new int[]{row, col+1});
rooms[row][col+1] = Math.min(rooms[row][col+1], level);
}
}
}
}
}
Code2
class Solution {
public void wallsAndGates(int[][] rooms) {
if (rooms == null || rooms.length == 0 || rooms[0] == null || rooms[0].length == 0) {
return;
}
Queue<int[]> queue = new LinkedList<>();
for (int i = 0; i < rooms.length; i++) {
for (int j = 0; j < rooms[0].length; j++) {
if (rooms[i][j] == 0) {
queue.offer(new int[]{i, j});
}
}
}
while (!queue.isEmpty()) {
int[] pos = queue.poll();
int row = pos[0];
int col = pos[1];
if (row - 1 >= 0 && rooms[row-1][col] != -1 && rooms[row-1][col] == Integer.MAX_VALUE) {
queue.offer(new int[]{row-1, col});
rooms[row-1][col] = rooms[row][col]+1;
}
if (row + 1 < rooms.length && rooms[row+1][col] != -1 && rooms[row+1][col] == Integer.MAX_VALUE) {
queue.offer(new int[]{row+1, col});
rooms[row+1][col] = rooms[row][col]+1;
}
if (col - 1 >= 0 && rooms[row][col-1] != -1 && rooms[row][col-1] == Integer.MAX_VALUE) {
queue.offer(new int[]{row, col-1});
rooms[row][col-1] = rooms[row][col]+1;
}
if (col + 1 < rooms[0].length && rooms[row][col+1] != -1 && rooms[row][col+1] == Integer.MAX_VALUE) {
queue.offer(new int[]{row, col+1});
rooms[row][col+1] = rooms[row][col]+1;
}
}
}
}
问题
给一个地图,里面包含门(0),墙(-1)和空间(INF)。计算每个空间到最近的门的距离(或者说到门的最近距离)。
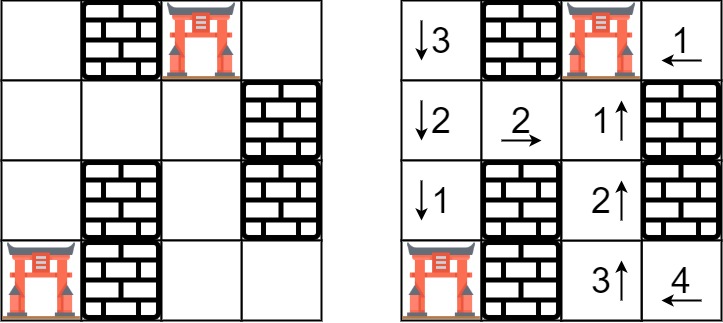
Input: rooms = [[2147483647,-1,0,2147483647],[2147483647,2147483647,2147483647,-1],[2147483647,-1,2147483647,-1],[0,-1,2147483647,2147483647]]
Output: [[3,-1,0,1],[2,2,1,-1],[1,-1,2,-1],[0,-1,3,4]]
算法
这个题目看起来就是用flood fill算法去做。遍历地图,遇到门之后做bfs,算出每个空间格子的距离,记录最小值。这里面对于每个门开始进行bfs,visited都是要重新设置,因为空格可以重复走。
但是这个算法的实现如代码1,最终的空间复杂度会是O(m*n*m*n),因为遍历一遍地图是O(mn),在对每个门进行遍历是O(mn)。平台会判TEL。
参考答案给了一种思路,可以将时间复杂度降下来到O(mn)。
具体思路就是在一开始就将所有的门记录在队列中,然后开始bfs,这样得到的结果就是最小值。比如例子中的[1, 0]位置,当第一遍从队列中取值的时候,即第一层遍历,会取到[3, 0]门位置的上面位置[2, 0]以及门[0, 2]下面的[1, 2],第二轮遍历的时候,[2, 0]位置下一个会遍历到[1, 0]位置,因此距离已经是最短。
可以这么理解,每一轮遍历都是从门向外扩散一圈(距离加一),距离即位最短。当其他门遇到这个位置的时候,以及有值且为最短,他不会再去赋值。
这个题目不像传统的flood fill算法是因为我们不是在计算连通性,而是对于每个空位置去做最短距离计算,整个棋盘的空位置会被重复走过,所以可以从所有的根(门)同时开始,会节省时间。而第200题,计算岛屿数量,我们一个个的计算,是因为当前的连通岛屿被计算过之后就不会重复计算。
代码1
class Solution {
public void wallsAndGates(int[][] rooms) {
if (rooms == null || rooms.length == 0 || rooms[0] == null || rooms[0].length == 0) {
return;
}
for (int i = 0; i < rooms.length; i++) {
for (int j = 0; j < rooms[0].length; j++) {
boolean[][] visited = new boolean[rooms.length][rooms[0].length];
if (rooms[i][j] == 0) {
bfs(rooms, i, j, visited);
}
}
}
}
private void bfs(int[][] rooms, int i, int j, boolean[][] visited) {
visited[i][j] = true;
Queue<int[]> queue = new LinkedList<>();
queue.offer(new int[]{i, j});
int level = 0;
while (!queue.isEmpty()) {
level++;
int size = queue.size();
for (int x = 0; x < size; x++) {
int[] pos = queue.poll();
int row = pos[0];
int col = pos[1];
if (row - 1 >= 0 && rooms[row-1][col] != -1 && !visited[row-1][col]) {
visited[row-1][col] = true;
queue.offer(new int[]{row-1, col});
rooms[row-1][col] = Math.min(rooms[row-1][col], level);
}
if (row + 1 < rooms.length && rooms[row+1][col] != -1 && !visited[row+1][col]) {
visited[row+1][col] = true;
queue.offer(new int[]{row+1, col});
rooms[row+1][col] = Math.min(rooms[row+1][col], level);
}
if (col - 1 >= 0 && rooms[row][col-1] != -1 && !visited[row][col-1]) {
visited[row][col-1] = true;
queue.offer(new int[]{row, col-1});
rooms[row][col-1] = Math.min(rooms[row][col-1], level);
}
if (col + 1 < rooms[0].length && rooms[row][col+1] != -1 && !visited[row][col+1]) {
visited[row][col+1] = true;
queue.offer(new int[]{row, col+1});
rooms[row][col+1] = Math.min(rooms[row][col+1], level);
}
}
}
}
}
代码2
class Solution {
public void wallsAndGates(int[][] rooms) {
if (rooms == null || rooms.length == 0 || rooms[0] == null || rooms[0].length == 0) {
return;
}
Queue<int[]> queue = new LinkedList<>();
for (int i = 0; i < rooms.length; i++) {
for (int j = 0; j < rooms[0].length; j++) {
if (rooms[i][j] == 0) {
queue.offer(new int[]{i, j});
}
}
}
while (!queue.isEmpty()) {
int[] pos = queue.poll();
int row = pos[0];
int col = pos[1];
if (row - 1 >= 0 && rooms[row-1][col] != -1 && rooms[row-1][col] == Integer.MAX_VALUE) {
queue.offer(new int[]{row-1, col});
rooms[row-1][col] = rooms[row][col]+1;
}
if (row + 1 < rooms.length && rooms[row+1][col] != -1 && rooms[row+1][col] == Integer.MAX_VALUE) {
queue.offer(new int[]{row+1, col});
rooms[row+1][col] = rooms[row][col]+1;
}
if (col - 1 >= 0 && rooms[row][col-1] != -1 && rooms[row][col-1] == Integer.MAX_VALUE) {
queue.offer(new int[]{row, col-1});
rooms[row][col-1] = rooms[row][col]+1;
}
if (col + 1 < rooms[0].length && rooms[row][col+1] != -1 && rooms[row][col+1] == Integer.MAX_VALUE) {
queue.offer(new int[]{row, col+1});
rooms[row][col+1] = rooms[row][col]+1;
}
}
}
}