52. N-Queens II & 51. N-Queens
Problems
Given a board of length n, construct a board on which queen pieces are placed so that they do not attack each other.
A queen can attack him on the same row, the same column or on the same diagonal.
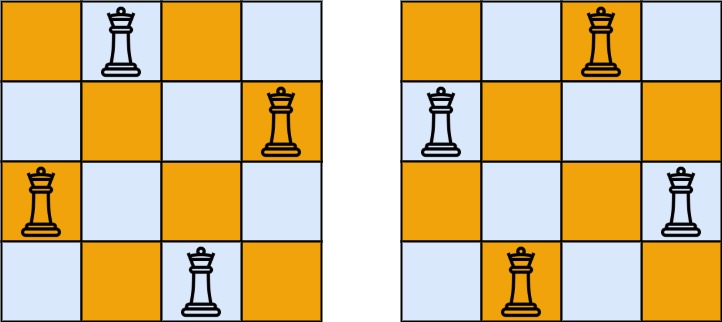
This example is given n is 4 and there are two answers.
Question 51 asks how many solutions there are, and question 52 asks which solutions are.
Algorithm
This question answers question 51 first, which is a more typical backtracking question. Because you need to place queens one by one on the board to see if it is OK to place them in that position. (Ignoring the code, we humans play the game in the same way)
First of all, we have to construct a board, which we have to do ourselves. Secondly, only one queen is placed at the beginning of each line, and if the position is reasonable, we continue to place it recursively, and if it is not reasonable, we go back to the previous step (backtracking here); then in the process, we record the layout of the board that can be placed at the end that is the answer.
In the marching process, it is necessary to judge whether this position can be put after each time a new queen is put, and this also needs to be realized.
The 52 questions is to put back the results of the 51 questions to calculatesize is the simplest method, or better directly each time you encounter a feasible answer plus one can, without recording the actual results.
The time complexity of the backtracking method is O(N!), because a huge decision tree is generated, the space complexity is O(N*N), we need to construct a chessboard.
Code1 and code2 is the code for question 51 and code3 is for question 52.
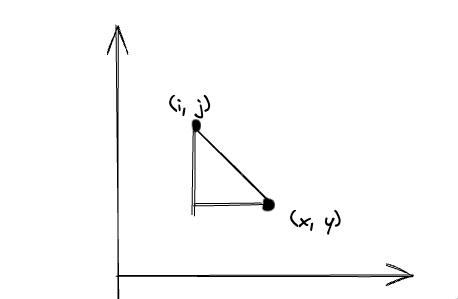
The main difference is the implementation if isValid(), in code1 I used a very naive implementation, however, there is a smarter way. I don't need to check the row below and column after the current row since we are doing this row by row, col by col. For the anti-diagonal and diagonal directions, the standard answer utilized slope, since the board is square, the dots on diagnose share same slope. So there would be a equationabs(x-i) = abs(y-j), from this we get
x - i = y - j;
x - i = j - y;
i - x = y - j;
i - x = j - y
and finally which is
x - y = i - j;
x + y = i + j;
Besides, we do it row by row so we don't have to care about the row before. And for column, if they are on the same column, j == y.
Code 1
class Solution {
List<List<String>> res = new ArrayList<>();
public List<List<String>> solveNQueens(int n) {
if (n == 0) return res;
char[][] board = constructBoard(n);
helper(board, 0);
return res;
}
private void helper(char[][] board, int row) {
int n = board.length;
if (row == n) {
List<String> list = new ArrayList<>();
for (char[] r : board) {
String s = new String(r);
list.add(s);
}
res.add(list);
return;
}
for (int i = 0; i < n; i++) {
board[row][i] = 'Q';
if (isValid(board)) {
helper(board, row + 1);
}
board[row][i] = '.';
}
}
private boolean isValid(char[][] board) {
int n = board.length;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (board[i][j] == 'Q') {
for (int x = 0; x < n; x++) {
if (board[x][j] == 'Q' && x != i) {
return false;
}
}
for (int x = 0; x < n; x++) {
if (board[i][x] == 'Q' && x != j) {
return false;
}
}
for (int x = 1; i-x >= 0 && j+x < n; x++) {
if (board[i-x][j+x] == 'Q') {
return false;
}
}
for (int x = 1; j-x >= 0 && i+x < n; x++) {
if (board[i+x][j-x] == 'Q') {
return false;
}
}
for (int x = 1; j+x < n && i+x < n; x++) {
if (board[i+x][j+x] == 'Q') {
return false;
}
}
for (int x = 1; j-x >= 0 && i-x >= 0; x++) {
if (board[i-x][j-x] == 'Q') {
return false;
}
}
}
}
}
return true;
}
private char[][] constructBoard(int n) {
char[][] board = new char[n][n];
for (char[] row : board) {
Arrays.fill(row, '.');
}
return board;
}
}
Code 2
class Solution {
List<List<String>> res = new ArrayList<>();
public List<List<String>> solveNQueens(int n) {
if (n == 0) return res;
char[][] board = constructBoard(n);
helper(board, 0);
return res;
}
private void helper(char[][] board, int row) {
int n = board.length;
if (row == n) {
List<String> list = new ArrayList<>();
for (char[] r : board) {
String s = new String(r);
list.add(s);
}
res.add(list);
return;
}
for (int i = 0; i < n; i++) {
if (board[row][i] == '.') {
board[row][i] = 'Q';
if (isValid(board, row, i)) {
helper(board, row + 1);
}
board[row][i] = '.';
}
}
}
private boolean isValid(char[][] board, int x, int y) {
int n = board.length;
for(int i = 0; i < x; i++) {
for(int j = 0; j < n; j++) {
if(board[i][j] == 'Q' && (x + j == y + i || x + y == i + j || j == y))
return false;
}
}
return true;
}
private char[][] constructBoard(int n) {
char[][] board = new char[n][n];
for (char[] row : board) {
Arrays.fill(row, '.');
}
return board;
}
}
Code 3
class Solution {
int res = 0;
public int totalNQueens(int n) {
if (n == 0) return res;
char[][] board = constructBoard(n);
helper(board, 0);
return res;
}
private void helper(char[][] board, int row) {
int n = board.length;
if (row == n) {
res++;
return;
}
for (int i = 0; i < n; i++) {
if (board[row][i] == '.') {
board[row][i] = 'Q';
if (isValid(board, row, i)) {
helper(board, row + 1);
}
board[row][i] = '.';
}
}
}
private boolean isValid(char[][] board, int x, int y) {
int n = board.length;
for(int i = 0; i < x; i++) {
for(int j = 0; j < n; j++) {
if (board[i][j] == 'Q' && (x-y == i-j || x+y == i+j || y == j)) {
return false;
}
}
}
return true;
}
private char[][] constructBoard(int n) {
char[][] board = new char[n][n];
for (char[] row : board) {
Arrays.fill(row, '.');
}
return board;
}
}
问题
给一个棋盘的长度n,构造一个棋盘在上放皇后棋子,使他们不会相互攻击到对方。
皇后可以攻击到他的同一行,同一列或者在同一个斜线上。
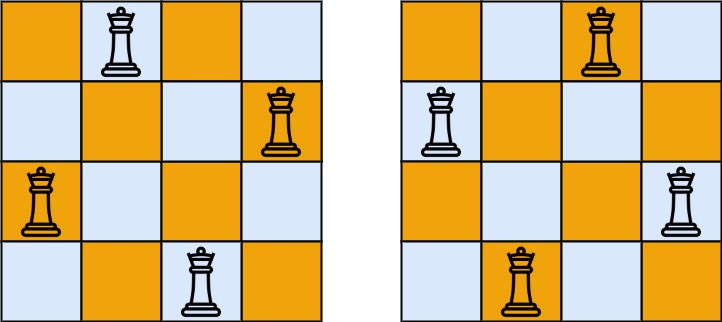
这个例子是给定n为4,有两个答案。
51题问的是有多少个解,52题问的是解是哪些。
算法
这个题目先解答51题,是比较典型的回溯题目。因为你需要在棋盘上一个个放置皇后来看放在这个位置是否可以。(不考虑写代码, 我们人类玩游戏也是这个思路)
首先要构筑一个棋盘,需要我们自己完成。其次每行开始只放一个,如果位置合理就递归的继续往下放,不合理就退回到上一步(这里是回溯);然后在这个过程中,记录可以放到最后的棋盘布局即为答案。
在行进过程中,需要在每一次放一个新的皇后之后判断这个位置是否可以放,这个也需要实现。
52题就是将51题的放回结果计算size是最简单的方法,或者好一点直接每次遇到可行答案加一即可,不记录实际结果。
回溯方法的时间复杂度是O(N!),因为产生了一个巨大的决策树,空间复杂度是O(N*N),我们需要构造一个棋盘。
代码1和代码2是问题51的代码,代码3是问题52的代码。
主要的区别是如果isValid()的实现,在代码1中我使用了一个非常幼稚的实现,然而,有一个更聪明的方法。我不需要检查当前行下面的行和后面的列,因为我们是逐行、逐列地进行的。对于反对角线和对角线方向,标准答案是利用斜率,因为棋盘是方形的,诊断上的点有相同的斜率。所以会有一个方程式abs(x-i)=abs(y-j),由此我们可以得到
x - i = y - j;
x - i = j - y;
i - x = y - j;
i - x = j - y
最后是
x - y = i - j;
x + y = i + j;
此外,我们逐行进行,所以我们不必关心之前的行。而对于列来说,如果它们在同一列,j == y。