10K's

Question

You are given an m x n integer matrix matrix with the following two properties:

• Each row is sorted in non-decreasing order.
• The first integer of each row is greater than the last integer of the previous row.

Given an integer target, return true if target is in matrix or false otherwise.

You must write a solution in O(log(m * n)) time complexity.

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -10^4 <= matrix[i][j], target <= 10^4

Algorithm

This is a typical binary search question. You have a strictly sorted array and you are asked to find the target. Now the array is segmented on a matrix, so you need to figure out how to map the 1D array index into a 2D array.

So basically, say we have a index mid in 1-D array, in the question, the matrix is

• Each row is sorted in non-decreasing order.
• The first integer of each row is greater than the last integer of the previous row.

So we could simply make

i = mid / n;
j = mid % n;

Like this:

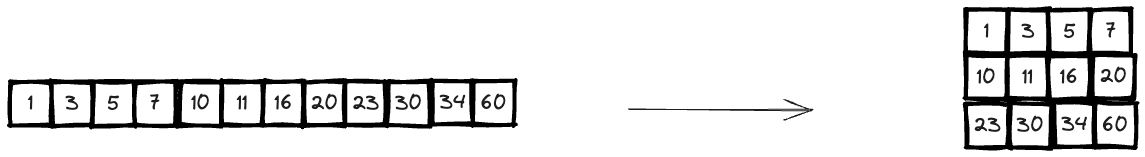
Code

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length;
        int n = matrix[0].length;
        int left = 0;
        int right = m * n;
        int mid, i, j;
        while (left < right) {
            mid = left + (right - left) / 2;
            i = mid / n;
            j = mid % n;
            if (target == matrix[i][j]) {
                return true;
            } else if (target > matrix[i][j]) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }
        return false;
    }
}