A Quick Note of Binary Index Tree
What is it
- A binary index tree, also known as a tree array, also known as Fenwick Tree, is still essentially an array that implements O(logn) time complex range queries and updates. It can be interpreted as better than segment tree in specific cases.
What problem is solved (application scenario)
-
Just like the emergence of the segment tree, a data structure emerged to solve recurring range queries and updates. There is a certain efficiency gain compared to using prefix sums (O(n) updates and queries).
-
The advantage is that it's faster in time, the disadvantage is that it's a little hard to understand.
Key points
lowbit
Define a function lowbit that finds the number of bits that a number goes through when it starts counting from the far right until it meets 1. This can be achieved in the code by bitwise operations
public int lowbit(int val) {
return val*(-val);
}
-
The bull's-eye is coming.
lowbit o ├ 1000 = 8 ┌───────┴───────┐ │ o o ├ 100 = 4 ┌───┴───┐ ┌───┴───┐ │ o o o o ├ 10 = 2 ┌─┴─┐ ┌─┴─┐ ┌─┴─┐ ┌─┴─┐ │ o o o o o o o o ├ 1 = 1 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 │
We can see patterns here, same level nodes have same ending.
- And when a node n is a right child, n - lowbit(n) is its parent: for example
12,12 - lowbit(12) = 12 - 4 = 8is exactly the parent8of12. And when a node is a left child, n - lowbit(n) is its grandfather: e.g. node10,10 - lowbit(10) = 10 - 2 = 8, is the left grandfather of 10. - When a node n is a right child, n + lowbit(n) is its grandfather node: for example,
6 + lowbit(6) = 6 + 2 = 8corresponds to the right grandfather node of 6; when a node n is a left child, n + lowbit(n) is its parent, for example, node4,4 + lowbit(4) = 4 + 4 = 8is the parent node of4. is the parent node of4. - You can also see that
n - lowbit(n) + 1corresponds to a node on a complete bifurcation, starting from the node corresponding to the number n and taking the left child of the node up to the node at the first level. For example, the node where12is located, keep taking the left child of the node, and you end up with9, and9 = 12 - 4 + 1 = 12 - lowbit(12) + 1. - With lowbit we can quickly locate in a complete binary tree.
Build the index
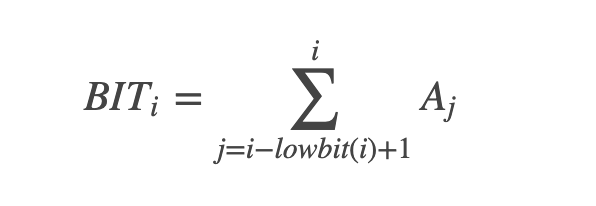
o
┌───────┴───────┐
o x
┌───┴───┐ ┌───┴───┐
o o x o
┌─┴─┐ ┌─┴─┐ ┌─┴─┐ ┌─┴─┐
o o o o x x o o
0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5
A: 2 1 3 1
BIT: (7)
You can see that 12 - lowbit(12) + 1 = 12-4+1=9, so BIT[12] = A[9] + A[10] + A[11] + A[12]. Similarly, to calculate BIT[8], we need to calculate A[1] + ... + A[8], since 8 - lowbit(8) + 1 = 1.
Principle and implementation
Summation
- With BIT, if we solve for sum(k), we just need to sum k and the left grandfather/parent node of k. The complexity is O(logn).
- Let's take
6for example,BIT[6]is equivalent toA[5] + A[6], but we have to computeA[1] + ... + A[6], so alsoA[1] + ... + A[4], which in BIT corresponds exactly toBIT[4]. Taking14as another example,BIT[14] = A[13] + a[14], which is still short ofA[1] + ... + A[12], so we find14 - lowbit(14) = 14 - 2 = 12, and sinceBIT[12] = BIT[9] + ... + BIT[12], so it is still short ofA[1] + ... + A[8], which exactly corresponds toBIT[8], and we have12 - lowbit(12) = 12 - 4 = 8.
So the sum(k) operation is to find the sum of node k and its parent node.
Update nodes
- From BIT's node-defining formula you can until that a certain value of the original array is updated, it affects all its right grandfather/parent nodes
- This can be obtained by
k + lowbit(k). For exampleA[9]has changed, and by definition we need to updateBIT[9], BIT[10], BIT[12]. This update can be implemented by lowbit(n)+n with a time complexity of O(nlogn).
Initialization
- With the help of the update operation, the update function is called to update each value. The complexity is O(nlogn).
import static org.junit.Assert.assertEquals;
/**
* Created by szhang on 2023/3/20
*/
public class BinaryIndexedTree {
int[] nums;
int[] tree;
public BinaryIndexedTree(int[] nums) {
this.nums = nums;
this.tree = new int[nums.length + 1];
for (int i = 0; i < nums.length; i++) {
update(i, nums[i]);
}
}
public void update(int i, int val) {
int diff = val - nums[i];
nums[i] = val;
for (int j = i + 1; j <= nums.length; j += j&(-j)) {
tree[j] += diff;
}
}
public int sumRange(int i, int j) {
return sum(j+1) - sum(i);
}
private int sum(int k) {
int sum = 0;
for (int i = k; i > 0; i -= i*(-i)) { // i*(-i) is the lowbit function
sum += tree[i];
}
return sum;
}
public static void main(String[] args) {
int[] nums = {1, 3, 2, 4, 5, 6};
BinaryIndexedTree bit = new BinaryIndexedTree(nums);
assertEquals(10, bit.sumRange(0, 2));
assertEquals(18, bit.sumRange(1, 4));
assertEquals(21, bit.sumRange(0, 5));
bit.update(2, 7);
assertEquals(15, bit.sumRange(0, 2));
assertEquals(24, bit.sumRange(1, 4));
assertEquals(28, bit.sumRange(0, 5));
}
}
Reference
是什么
- 二叉索引树,也称树状数组,又称Fenwick Tree,本质上还是一个数组,实现了O(logn)时间复杂的的范围查询和更新。可以理解为特定情况下比segment tree好用。
解决了什么问题(应用场景)
-
正如segment tree的出现类似,为了解决**经常性的范围查询和更新**,而出现的一种数据结构。相比于使用前缀和(O(n)的更新和查询),会有一定的效率提升。
-
优点在于时间上更快了,缺点就是有一点点难以理解。
关键点
lowbit
定义一个函数lowbit,他求的一个数是从最右边开始数直到遇到1时候走过的位数。在代码中可以通过位运算来实现
public int lowbit(int val) {
return val*(-val);
}
-
牛逼的东西要来了:
lowbit o ├ 1000 = 8 ┌───────┴───────┐ │ o o ├ 100 = 4 ┌───┴───┐ ┌───┴───┐ │ o o o o ├ 10 = 2 ┌─┴─┐ ┌─┴─┐ ┌─┴─┐ ┌─┴─┐ │ o o o o o o o o ├ 1 = 1 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 │我们可以看到这个不同层数的二叉结尾是有规律的。
- 而且当一个节点n是右孩子的时候,n - lowbit(n)是他的父节点: 例如
12,12 - lowbit(12) = 12 - 4 = 8正好是12的父节点8。而当一个节点是左孩子的时候,n - lowbit(n)是他的祖父节点: 例如节点10,10 - lowbit(10) = 10 - 2 = 8,是 10 的左祖父节点。 - 当一个节点n是右孩子的时候,n + lowbit(n)是他的祖父节点:例如
6 + lowbit(6) = 6 + 2 = 8则对应于 6 的右祖父节点;当一个节点n是左孩子的时候, n+lowbit(n)是他的父节点,例如节点4,4 + lowbit(4) = 4 + 4 = 8是4的父节点。 - 同时可以看到
n - lowbit(n) + 1在完全二叉数上对应的节点,就是从数字 n 对应的节点开始,不断取节点的左子节点直到第一层的那个节点。例如12所在的结点,不断取左子节点,最终得到的是9,而9 = 12 - 4 + 1 = 12 - lowbit(12) + 1。 - 有了lowbit我们就可以在完全二叉树中快速定位。
- 而且当一个节点n是右孩子的时候,n - lowbit(n)是他的父节点: 例如
建立索引
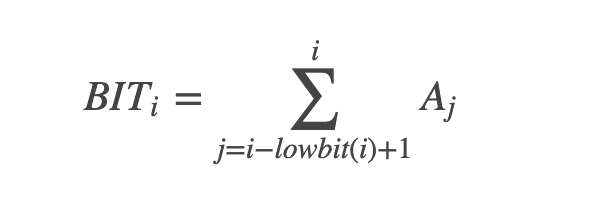
o
┌───────┴───────┐
o x
┌───┴───┐ ┌───┴───┐
o o x o
┌─┴─┐ ┌─┴─┐ ┌─┴─┐ ┌─┴─┐
o o o o x x o o
0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5
A: 2 1 3 1
BIT: (7)
可以看到 12 - lowbit(12) + 1 = 12-4+1=9,因此 BIT[12] = A[9] + A[10] + A[11] + A[12]。同理,如果要计算 BIT[8],则需要计算 A[1] + ... + A[8],因为 8 - lowbit(8) + 1 = 1。
原理和实现
求和
- 有了BIT之后,如果求sum(k),我们只需要将k和k的左祖父/父节点相加即可。复杂度是O(logn)。
- 我们以
6为例,BIT[6]相当于A[5] + A[6],但我们要计算A[1] + ... + A[6],因此还要计算A[1] + ... + A[4],而在 BIT 中,这正好对应于BIT[4]。再以14为例,BIT[14] = A[13] + a[14],还差A[1] + ... + A[12],于是找到14 - lowbit(14) = 14 - 2 = 12,而由于BIT[12] = BIT[9] + ... + BIT[12],因此还差A[1] + ... + A[8],正好对应于BIT[8],而又有12 - lowbit(12) = 12 - 4 = 8。
所以说 sum(k) 操作就是求节点 k 及它的父节点的和。
更新节点
- 从BIT的节点定义公式可以直到,原数组某个数值更新,会影响其所有的右祖父/父节点
- 这可以通过
k + lowbit(k)来得到。例如A[9]发生了变化,根据定义,我们需要更新BIT[9], BIT[10], BIT[12]。这个更新的过程可以通过lowbit(n)+n来实现,时间复杂度为O(nlogn)。
初始化
- 借助update操作,调用update函数更新每个数值。复杂度为 O(nlogn)。
import static org.junit.Assert.assertEquals;
/**
* Created by szhang on 2023/3/20
*/
public class BinaryIndexedTree {
int[] nums;
int[] tree;
public BinaryIndexedTree(int[] nums) {
this.nums = nums;
this.tree = new int[nums.length + 1];
for (int i = 0; i < nums.length; i++) {
update(i, nums[i]);
}
}
public void update(int i, int val) {
int diff = val - nums[i];
nums[i] = val;
for (int j = i + 1; j <= nums.length; j += j&(-j)) {
tree[j] += diff;
}
}
public int sumRange(int i, int j) {
return sum(j+1) - sum(i);
}
private int sum(int k) {
int sum = 0;
for (int i = k; i > 0; i -= i*(-i)) { // i*(-i) is the lowbit function
sum += tree[i];
}
return sum;
}
public static void main(String[] args) {
int[] nums = {1, 3, 2, 4, 5, 6};
BinaryIndexedTree bit = new BinaryIndexedTree(nums);
assertEquals(10, bit.sumRange(0, 2));
assertEquals(18, bit.sumRange(1, 4));
assertEquals(21, bit.sumRange(0, 5));
bit.update(2, 7);
assertEquals(15, bit.sumRange(0, 2));
assertEquals(24, bit.sumRange(1, 4));
assertEquals(28, bit.sumRange(0, 5));
}
}