A Quick Note of Trie

What it is

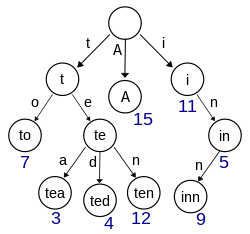
Trie is a special form of n-ary search tree; a data structure used for locating specific keys from within a set.(often strings)
Normally each node only store one char and root is empty, to get the full text or word, you traverse in DFS to construct or search;
Used for prefex matching（full text search), spell check, search bar prompt;
Also called prefix tree;

Pros

Compared with list, search a word in a list time complexity is O(n*word.length), to binary search tree, search time complexity is O(logn), while the time complexity for trie is O(word.length)

Cons

It's a space and time trade off. The space complexity is O(number of trie node * 26) or O(number of words * words.length * 26), if there is only lower letter in the words.

Implementation

We need to construct the trie and its nodes first and then do the search. There tends to be some extra fields defined in the nodes depends on the usage.

Normally there are three operations:

Search/contains

We are given a key(word) and we traverse each character in the key in order and see if they are in the trie and if child of previous node.

Trie-Find(x, key)
    for 0 ≤ i < key.length do
        if x.Children[key[i]] = nil then
            return false
        end if
        x := x.Children[key[i]]
    repeat
    return x.Value

Add/insert
```
Trie-Insert(x, key, value)
    for 0 ≤ i < key.length do
        if x.Children[key[i]] = nil then
            x.Children[key[i]] := Node()
        end if
        x := x.Children[key[i]]
    repeat
    x.Value := value
    x.Is-Terminal := True
```
Here we do almost the same thing in search, but when we find a character in key is not in the trie, we construct a new node and add it to its parents' children.

It is worth to notice that we have a is-terminal to mark a node that form root to that node there is a word(key).

Code

public class TrieNode {
    // Character c; the character the trieNode represents
    TrieNode[] children; // Map<Character, Trie> map;
    boolean isWord; // or isTerminal;
    // String word; the word it represents;

    public TrieNode() {
        children = new TrieNode[26]; // assume it only contains lower letter char;
        isWord = false;
    }

    public TrieNode[] getChildren() {
        return children;
    }

    public void setChildren(TrieNode[] children) {
        this.children = children;
    }

    public boolean getIsWord() {
        return isWord;
    }

    public void setIsWord(boolean word) {
        isWord = word;
    }
}

public class Trie {
    TrieNode root;

    public Trie() {
        root = new TrieNode();
    }

    public void add(String word) {
        TrieNode curNode = root;
        for (Character c : word.toCharArray()) {
            if (curNode.children[c-'a'] == null) {
                curNode.children[c-'a'] = new TrieNode();
            }
            curNode = curNode.children[c-'a'];
        }
        curNode.isWord = true;
    }

    public boolean contains(String word) {
        TrieNode curNode = root;
        for (Character c : word.toCharArray()) {
            if (curNode.children[c-'a'] == null) {
                return false;
            }
            curNode = curNode.children[c-'a'];
        }
        return curNode.getIsWord();
    }

    public boolean startsWith(String prefix) {
        TrieNode curNode = root;
        for (Character c : prefix.toCharArray()) {
            if (curNode.children[c-'a'] == null) {
                return false;
            }
            curNode = curNode.children[c-'a'];
        }
        return true;
    }
}

10K's