Random All In One - 398. Random Pick Index&384. Shuffle an Array&382. Linked List Random Node&380. Insert Delete GetRandom O(1)&138. Copy List with Random Pointer

这篇文章会涉及到随机算法的Leetcode题目，包括在有限数据集中随机选取n个元素，在无限数据集中随机选取一个元素，在无限数据中随机选取多个元素等。涉及到蓄水池算法，洗牌算法等。

题目1

398. Random Pick Index

Given an integer array nums with possible duplicates, randomly output the index of a given target number. You can assume that the given target number must exist in the array.

Implement the Solution class:

Solution(int[] nums) Initializes the object with the array nums.
int pick(int target) Picks a random index i from nums where nums[i] == target. If there are multiple valid i's, then each index should have an equal probability of returning.

Example 1:

Input
["Solution", "pick", "pick", "pick"]
[[[1, 2, 3, 3, 3]], [3], [1], [3]]
Output
[null, 4, 0, 2]

Explanation
Solution solution = new Solution([1, 2, 3, 3, 3]);
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
solution.pick(1); // It should return 0. Since in the array only nums[0] is equal to 1.
solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.

Constraints:

1 <= nums.length <= 2 * 104
-231 <= nums[i] <= 231 - 1
target is an integer from nums.
At most 104 calls will be made to pick.

算法1-直接随机数

这个题目是希望我们在有限数据集中随机选取某一个target数值的索引index。因为存在重复的元素，所以index也就不止一个，题目希望随机选取。

最开始考虑这种题目，我们想到的可能就是：在一个数据集中抽元素，抽中即可。所以有如下代码，我们获取到所有可能得索引，然后借助Java的random类在这些index中随机抽取一个即可。

代码1

class Solution {
    Random rdm;
    int[] nums;
    

    public Solution(int[] nums) {
        rdm = new Random();
        this.nums = nums;
    }
    
    public int pick(int target) {
        List<Integer> indexes = new ArrayList<>();
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] == target) {
                indexes.add(i);
            }
        }
        return indexes.get(rdm.nextInt(indexes.size()));
    }
}

/**
 * Your Solution object will be instantiated and called as such:
 * Solution obj = new Solution(nums);
 * int param_1 = obj.pick(target);
 */

题目2

384. Shuffle an Array

Given an integer array nums, design an algorithm to randomly shuffle the array. All permutations of the array should be equally likely as a result of the shuffling.

Implement the Solution class:

Solution(int[] nums) Initializes the object with the integer array nums.
int[] reset() Resets the array to its original configuration and returns it.
int[] shuffle() Returns a random shuffling of the array.

Example 1:

Input
["Solution", "shuffle", "reset", "shuffle"]
[[[1, 2, 3]], [], [], []]
Output
[null, [3, 1, 2], [1, 2, 3], [1, 3, 2]]

Explanation
Solution solution = new Solution([1, 2, 3]);
solution.shuffle();    // Shuffle the array [1,2,3] and return its result.
                       // Any permutation of [1,2,3] must be equally likely to be returned.
                       // Example: return [3, 1, 2]
solution.reset();      // Resets the array back to its original configuration [1,2,3]. Return [1, 2, 3]
solution.shuffle();    // Returns the random shuffling of array [1,2,3]. Example: return [1, 3, 2]

Constraints:

1 <= nums.length <= 50
-106 <= nums[i] <= 106
All the elements of nums are unique.
At most 104 calls in total will be made to reset and shuffle.

算法2-洗牌算法

这个题目看起来和随机不太关联，但是换个思路想，打乱一个数组==把一个数组的每个位置随机选一个原来数组元素放置。这个题目中就是k=nums.length。

对于题目1，我们只需要随机选择一个或者一次，但是对于要求随机选取多个或者多次的题目，按照之前的选取方法，可能会出现一个元素被重复选中的情况。

这时的算法可能会成为：当第一次选中时-> ok; 被重复选中->再抽一次。假设总共有n个值，我们需要选取m个，这个算法的缺点在于如果m比较接近n的话，重复的几率就会很大，时间复杂度就会变高。

然后我们会发现有一个**洗牌算法。**同样对于有限数据集，随机选取k个元素。

算法如下：

从给定数组data，范围为[0, n)，我们遍历data，当索引为i的时候，
从后面所有元素[i+1, n)中随机选取一个数data[j]和当前元素交换即可。

代码2

class Solution {
    int[] nums;
    Random rdm = new Random();

    public Solution(int[] nums) {
        this.nums = nums;
    }
    
    public int[] reset() {
        return nums;
    }
    
    public int[] shuffle() {
        int[] res = Arrays.copyOf(nums, nums.length);
        for (int i = 0; i < nums.length; i++) {
            int j = i + rdm.nextInt(nums.length - i);
            swap(res, i, j);
        }
        return res;
    }
    
    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

/**
 * Your Solution object will be instantiated and called as such:
 * Solution obj = new Solution(nums);
 * int[] param_1 = obj.reset();
 * int[] param_2 = obj.shuffle();
 */

对于16行，如果我们想要获取[i, n)的随机数，那么可以通过获取[0, n-i) + i来获取。

公式

要取得 [a,b) 的随机整数，使用 (rand () % (b-a))+ a;

要取得 [a,b] 的随机整数，使用 (rand () % (b-a+1))+ a;

要取得 (a,b] 的随机整数，使用 (rand () % (b-a))+ a + 1;

通用公式 a + rand () % n；其中的 a 是起始值，n 是整数的范围。

要取得 a 到 b 之间的随机整数，另一种表示：a + (int) b * rand () / (RAND_MAX + 1)。

要取得 0～1 之间的浮点数，可以使用 rand () /double (RAND_MAX)。

对应上述题目，rand()%n就是Java中的rdm.nextInt()的结果。

分析洗牌算法正确性的准则：产生的结果必须有 n! 种可能。这个很好解释，因为一个长度为 n 的数组的全排列就有 n! 种，也就是说打乱结果总共有 n! 种。算法必须能够反映这个事实，才是正确的。

有了这个原则再看代码应该就容易理解了：

对于 nums[0]，我们把它随机换到了索引 [0, n) 上，共有 n 种可能性；

对于 nums[1]，我们把它随机换到了索引 [1, n) 上，共有 n - 1 种可能性；

对于 nums[2]，我们把它随机换到了索引 [2, n) 上，共有 n - 2 种可能性；

以此类推，该算法可以生成 n! 种可能的结果，所以这个算法是正确的，能够保证随机性。

题目3

398. Random Pick Index

算法3-蓄水池算法（随机选取一个）

如果题目的输入成为了数据集大小n是未知的，比如他是一个stream，持续有数据进来。我们希望选取1个随机元素。

我们期望只将数据流遍历一遍就得到所选取的元素，并且得到的元素是随机的。要求就是每个元素被选取的概率是1/n。

算法：以1/i的概率选择第i个元素。

数学推导

每一个被选中的概率如下：第一个是当前元素被选的概率，因为我们只选一个，所以乘的是后面元素不被选择的概率。可得针对第i个元素，被选中的概率满足要求的1/n。

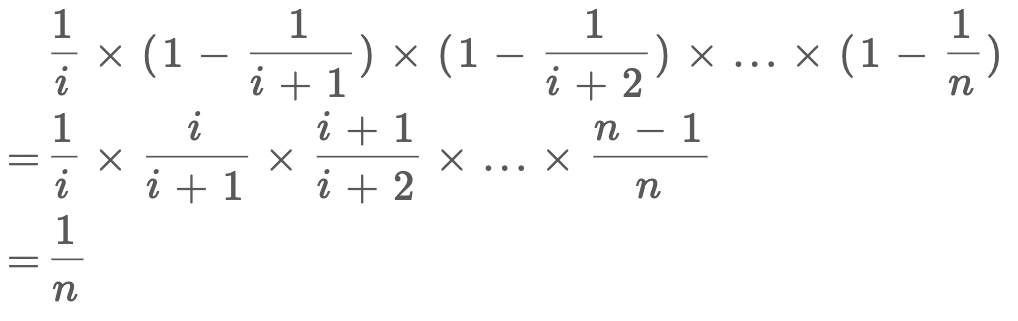
代码3

class Solution {
    Random rdm = new Random();
    int[] nums;
    

    public Solution(int[] nums) {
        this.nums = nums;
    }
    
    public int pick(int target) {
        int res = -1;
        int count = 0;
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] != target) {
                continue;
            }
            count++;
            if (rdm.nextInt(count) == 0) { // here we only pick the first one
                res = i;
            }
        }
        return res;
    }
}

/**
 * Your Solution object will be instantiated and called as such:
 * Solution obj = new Solution(nums);
 * int param_1 = obj.pick(target);
 */

题目4

算法4-蓄水池算法（随机选取多个）

要求随机选取m个元素。即要求每个元素的被选取的概率是m/n。

算法：前m个元素放入蓄水池，到第k个时(k>m)，按照m/k的概率选中当前元素，以均等的概率替换蓄水池中先前被选中的任一元素。

数学推导

第m个元素被选中的概率为当前元素被选中的概率*（之后元素不被选中的概率 + 之后被选中但不替换的概率）最终得到p=m/n。

或者借助算法3的推导，区别在于后面的元素都乘了1/k。因为虽然每次更细选择的概率大了k倍，但是具体的第i个元素还是要乘1/k，回到上一个推导了。

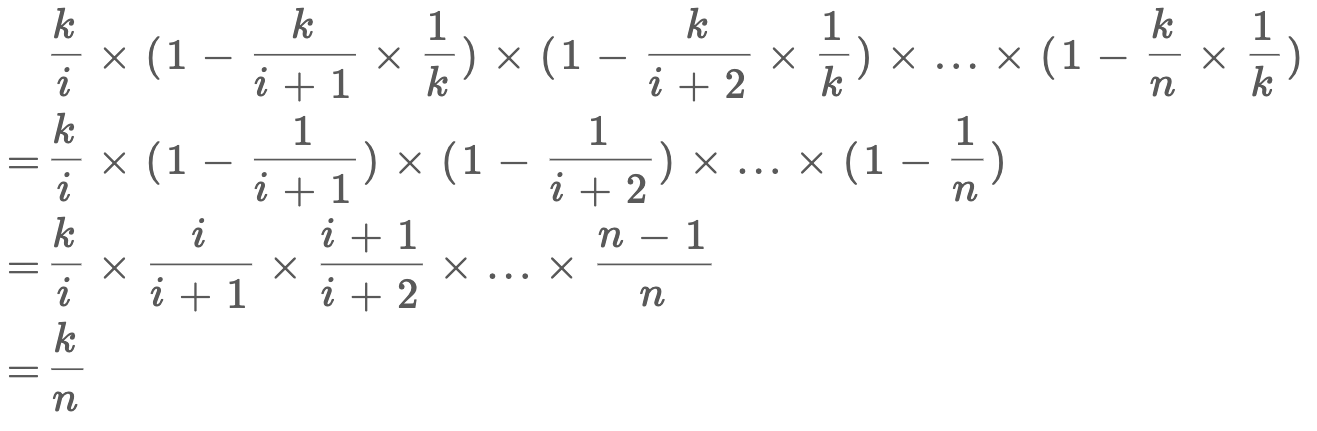
代码4

import java.util.Random;

public class ReserviorSampling {
    public int[] reserviorSampling(int[] stream, int k) {
        Random random = new Random();
        int[] res = new int[k];
        for (int i = 0; i <= k; i++) {
            res[i] = stream[i];
        }

        for (int i = k; i < stream.length; i++) {
            int rand = random.nextInt(i+1);
            if (rand < k) { //the probability of i < k is k/i
                res[rand] = stream[i];
            }
        }

        return res;
    }

}

题目5

382. Linked List Random Node

Given a singly linked list, return a random node's value from the linked list. Each node must have the same probability of being chosen.

Implement the Solution class:

Solution(ListNode head) Initializes the object with the head of the singly-linked list head.
int getRandom() Chooses a node randomly from the list and returns its value. All the nodes of the list should be equally likely to be chosen.

Example 1:

Input
["Solution", "getRandom", "getRandom", "getRandom", "getRandom", "getRandom"]
[[[1, 2, 3]], [], [], [], [], []]
Output
[null, 1, 3, 2, 2, 3]

Explanation
Solution solution = new Solution([1, 2, 3]);
solution.getRandom(); // return 1
solution.getRandom(); // return 3
solution.getRandom(); // return 2
solution.getRandom(); // return 2
solution.getRandom(); // return 3
// getRandom() should return either 1, 2, or 3 randomly. Each element should have equal probability of returning.

Constraints:

The number of nodes in the linked list will be in the range [1, 104].
-104 <= Node.val <= 104
At most 104 calls will be made to getRandom.

Follow up:

What if the linked list is extremely large and its length is unknown to you?
Could you solve this efficiently without using extra space?

算法5

和算法4同样的题目，只是数据结构使用链表。思路可以使用无限数据集选择一个元素的思路。满足Follow up的要求（不使用额外空间，链表很长且长度未知）。

代码5

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    Random random = new Random();
    ListNode head;

    public Solution(ListNode head) {
        this.head = head;
    }
    
    public int getRandom() {
        int res = -1;
        int count = 0;
        ListNode cur = head;
        while (cur != null) {
            count++;
            if (random.nextInt(count) == 0) {
                res = cur.val;
            }
            cur = cur.next;
        }
        return res;
    }
}

/**
 * Your Solution object will be instantiated and called as such:
 * Solution obj = new Solution(head);
 * int param_1 = obj.getRandom();
 */

题目6

380. Insert Delete GetRandom O(1)

Implement the RandomizedSet class:

RandomizedSet() Initializes the RandomizedSet object.
bool insert(int val) Inserts an item val into the set if not present. Returns true if the item was not present, false otherwise.
bool remove(int val) Removes an item val from the set if present. Returns true if the item was present, false otherwise.
int getRandom() Returns a random element from the current set of elements (it's guaranteed that at least one element exists when this method is called). Each element must have the same probability of being returned.

You must implement the functions of the class such that each function works in average O(1) time complexity.

Example 1:

Input
["RandomizedSet", "insert", "remove", "insert", "getRandom", "remove", "insert", "getRandom"]
[[], [1], [2], [2], [], [1], [2], []]
Output
[null, true, false, true, 2, true, false, 2]

Explanation
RandomizedSet randomizedSet = new RandomizedSet();
randomizedSet.insert(1); // Inserts 1 to the set. Returns true as 1 was inserted successfully.
randomizedSet.remove(2); // Returns false as 2 does not exist in the set.
randomizedSet.insert(2); // Inserts 2 to the set, returns true. Set now contains [1,2].
randomizedSet.getRandom(); // getRandom() should return either 1 or 2 randomly.
randomizedSet.remove(1); // Removes 1 from the set, returns true. Set now contains [2].
randomizedSet.insert(2); // 2 was already in the set, so return false.
randomizedSet.getRandom(); // Since 2 is the only number in the set, getRandom() will always return 2.

Constraints:

-231 <= val <= 231 - 1
At most 2 * ``105 calls will be made to insert, remove, and getRandom.
There will be at least one element in the data structure when getRandom is called.

算法6

这道题的关键点在于，所有的操作都需要是O(1)时间复杂度。且，geRandom还要返回一个随机元素。这道题和之前的题目其实没太大关系，主要是一个实现题目。

对于第一个点，操作需要在常数时间复杂度实现，可以用Hashmap， hashset，但是由于他们的内部结构涉及到哈希函数，哈希之后也是通过链表存储的，且可能存在哈希冲突，所以没办法做到等概率实现getRandom在常数时间。所以必须使用数组。

但是对于数组，插入和删除，必须要在尾部才可以满足常数时间的操作。所以对于删除，我们要将元素先换到尾部，再去做删除操作。交换元素涉及到元素的索引，为了满足常数时间找到元素的索引，我们还需要一个map存取每个元素的索引。

代码6

class RandomizedSet {
    Map<Integer, Integer> map;
    List<Integer> list;
    Random random = new Random();

    public RandomizedSet() {
        map = new HashMap<>();
        list = new ArrayList<>();
    }
    
    public boolean insert(int val) {
        if (map.containsKey(val)) {
            return false;
        }
        list.add(val);
        map.put(val, list.size() - 1);
        return true;
    }
    
    public boolean remove(int val) {
        if (!map.containsKey(val)) {
            return false;
        }
        int indexToRemove = map.remove(val);
        int lastValue = list.remove(list.size() - 1);
        if (indexToRemove != list.size()) { // when deleting the non-last element, you do swap
            list.set(indexToRemove, lastValue);
            map.put(lastValue, indexToRemove);
        }
        return true;
    }
    
    public int getRandom() {
        return list.get(random.nextInt(list.size()));
    }
}

/**
 * Your RandomizedSet object will be instantiated and called as such:
 * RandomizedSet obj = new RandomizedSet();
 * boolean param_1 = obj.insert(val);
 * boolean param_2 = obj.remove(val);
 * int param_3 = obj.getRandom();
 */

补充：蒙特卡洛验证法

往一个正方形里面随机打点，这个正方形里紧贴着一个圆，告诉你打点的总数和落在圆里的点的数量，让你计算圆周率。当打的点足够多的时候，点的数量就可以近似代表图形的面积。结合面积公式，可以很容易通过正方形和圆中点的数量比值推出圆周率的。
所以题目最终对于随机的验证，可能也是通过这种方法，做大量的输入，然后记录每个输出的随机数出现的次数，大致是相同的，或者说近似相等，则这个随机算法是可行的。

问题8

138. Copy List with Random Pointer

A linked list of length n is given such that each node contains an additional random pointer, which could point to any node in the list, or null.

Construct a deep copy of the list. The deep copy should consist of exactly n brand new nodes, where each new node has its value set to the value of its corresponding original node. Both the next and random pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. None of the pointers in the new list should point to nodes in the original list.

For example, if there are two nodes X and Y in the original list, where X.random --> Y, then for the corresponding two nodes x and y in the copied list, x.random --> y.

Return the head of the copied linked list.

The linked list is represented in the input/output as a list of n nodes. Each node is represented as a pair of [val, random_index] where:

val: an integer representing Node.val
random_index: the index of the node (range from 0 to n-1) that the random pointer points to, or null if it does not point to any node.

Your code will only be given the head of the original linked list.

Example 1:

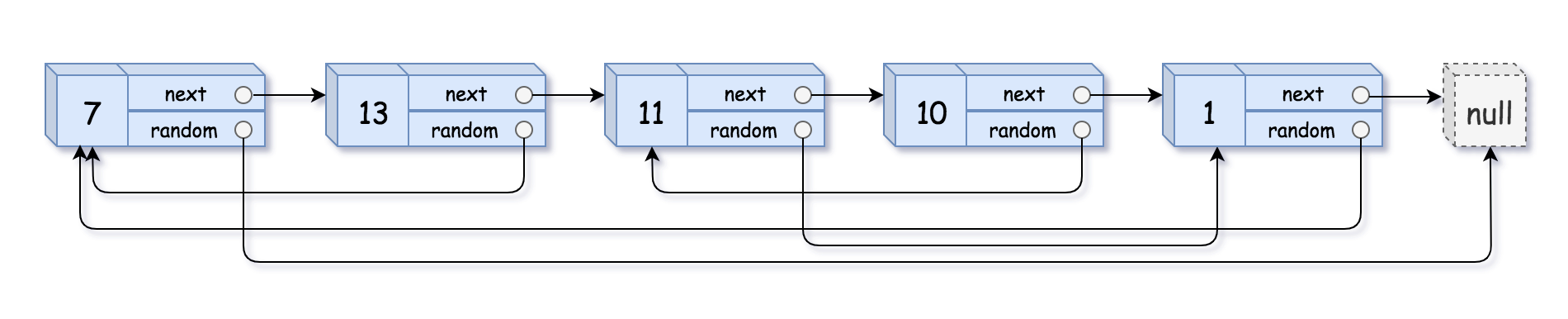
Input: head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
Output: [[7,null],[13,0],[11,4],[10,2],[1,0]]

算法8

这个题目是说，给一个链表，深复制它。这个链表特别的地方在于，不仅有一个next指针指向下一个元素，还有一个random指针指向链表中的其他元素，或者不指向元素（也就是null）。所以当复制的时候这个指针也要被复制。

这个题目需要记录每个node的位置或者是新旧节点的对应情况，这样才可以在取得一个节点的时候看是否它有对应的新节点产生，有则找到，没有则帮他新建一个（深拷贝）。然后依次遍历原来的链表，进行复制。

代码8-1

/*
// Definition for a Node.
class Node {
    int val;
    Node next;
    Node random;

    public Node(int val) {
        this.val = val;
        this.next = null;
        this.random = null;
    }
}
*/

class Solution {
    Map<Node, Node> map = new HashMap<>();
    public Node copyRandomList(Node head) {
        
        if (head == null) {
            return head;
        }
        Node cur = head;
        Node newNode = new Node(cur.val);
        map.put(head, newNode);
        
        Node newCur = newNode;
        
        while (cur != null) {
            newCur.next = getClonedNode(cur.next);
            newCur.random = getClonedNode(cur.random);
            cur = cur.next;
            newCur = newCur.next;
        }
        return newNode;
        
    }
    
    private Node getClonedNode(Node node) {
        if (node != null) {
            if (map.containsKey(node)) {
                return map.get(node);
            } else {
                Node newNode = new Node(node.val);
                map.put(node, newNode);
                return newNode;
            }
        }
        return null;
    }
}

算法8-2

上面的代码时间和空间复杂度都是O(n)，这个我们可以有一个算法让空间优化到O(1)。

你想我们为了保存新旧节点的对应关系，我们使用了字典，有一个对应关系，但是对于链表来说它本身就有一个指针结构。

这个方法比较取巧。利用链表本身的指针结构next，对于每一个节点在其后插入他的新节点，最后取新节点连成一个新的链表即可。

思路有了，方向有了，代码就好写了，就是一些链表的插入删除。遍历每一个节点，对他新生成一个影子节点，然后插入在其后。生成影子节点之后，再次遍历，关联random节点。最后将影子节点拆出来。

这个解法的点在于他更改了输入。对比前一个解法。

代码8-2

/*
// Definition for a Node.
class Node {
    int val;
    Node next;
    Node random;

    public Node(int val) {
        this.val = val;
        this.next = null;
        this.random = null;
    }
}
*/

class Solution {
    public Node copyRandomList(Node head) {
        if (head == null) {
            return head;
        }
        
        // insert shadow node
        Node cur = head;
        while (cur != null) {
            Node next = cur.next;
            cur.next = new Node(cur.val);
            cur.next.next = next;
            cur = cur.next.next;
        }
        
        // link random
        cur = head;
        while (cur != null) {
            cur.next.random = cur.random != null ? cur.random.next : null;
            cur = cur.next.next;
        }
        
        // unwave linkedlist;
        cur = head;
        Node newCur = head.next;
        Node newHead = head.next;
        while (cur != null) {
            cur.next = cur.next.next;
            newCur.next = newCur.next != null ? newCur.next.next : null;
            cur = cur.next;
            newCur = newCur.next;
        }
        return newHead;
    }
}

问题9

528. Random Pick with Weight

给一组数字，实现一下randomPick，但是这组数字有权重的，所以选择的时候也要参考权重。

算法9

带权重、轮盘赌、彩票算法这些题目。原来让我们随机选择，那么每个被选中的概率就是1/n，现在有权重，要参考每个的权重。

这种题目我也是看了参考答案。没想出来这种方法。算法其实就是对每个数字也就是他们自己的权重构建前缀和数组，然后以最大值为边界选取随机数，找到随机数出现在的区域，那个区域的右边界（前缀和的索引）即为返回的结果。

为什么前缀和呢？这么一看就明了了。我们的随机取数字，就是相当于扔一个石头，落在哪个颜色就选哪个数字。不同的颜色有不同的长度（权重）。

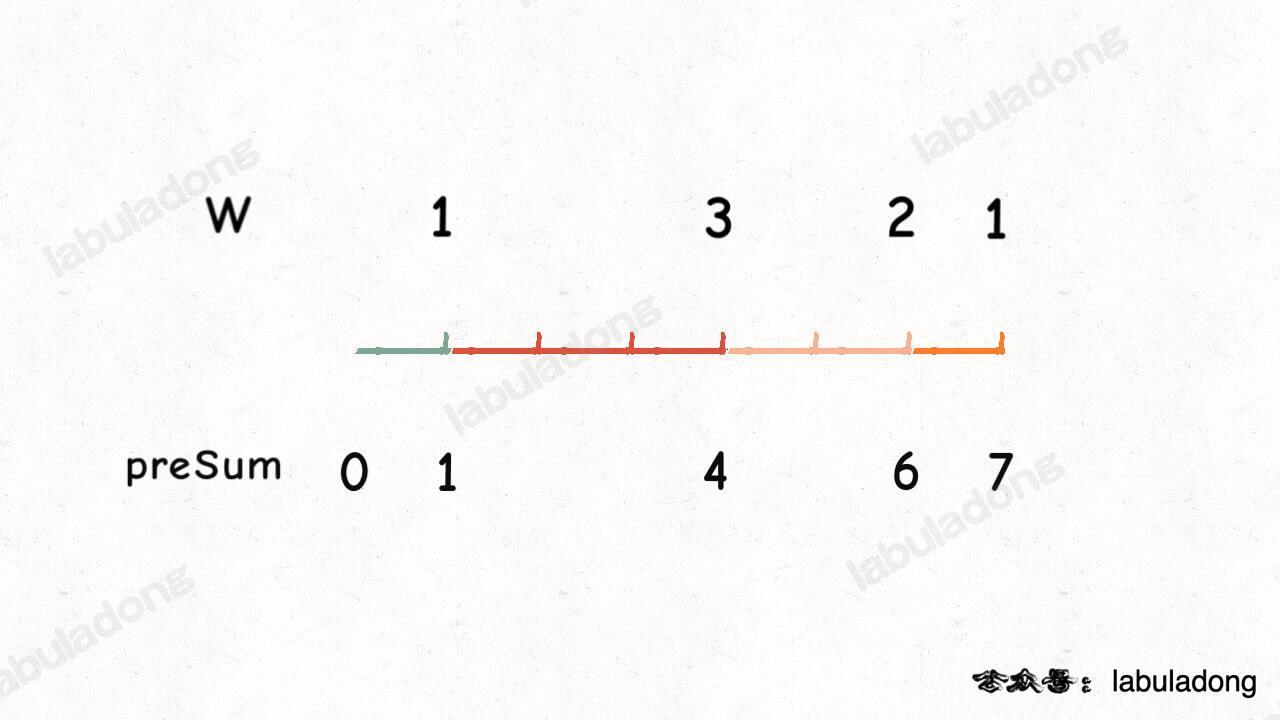
构建了前缀和，我们就要找生成的随机数落在哪个颜色区间，取区间的边界值。这个题目就成了，给定一个数组，找target值的索引，如果没找到，返回距离他最近的大于他的值的index。最后index 因为是在前缀和数组，给0和预留了一位，所以要把最后的结果减一以对应原来的数组nums。

代码9

class Solution {
    int[] nums;
    int[] preSums;
    Random random = new Random();

    public Solution(int[] w) {
        nums = w;
        preSums = new int[w.length+1];
        for (int i = 1; i <= nums.length; i++) {
            preSums[i] = preSums[i-1] + nums[i-1];
        }
    }
    
    public int pickIndex() {
        int rand = random.nextInt(preSums[preSums.length - 1]) + 1;
        int left = 0;
        int right = preSums.length;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (rand <= preSums[mid]) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left-1;
    }
}

/**
 * Your Solution object will be instantiated and called as such:
 * Solution obj = new Solution(w);
 * int param_1 = obj.pickIndex();
 */

参考

随机数专题总结

10K's